作业三
T1: 曲线拟合
题目
使用曲线模型
使用scipy模块中的curve_fit函数进行拟合,代码如下:
py
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
# raw data
xi = np.array([0.1, 0.2, 0.3, 0.4, 0.5,
0.6, 0.7, 0.8, 0.9])
yi = np.array([0, 2.122, 3.0244, 3.2568, 3.1399,
2.8579, 2.514, 2.1639, 1.8358])
# use g(x)=c1+c2x+c3sin(pi*x)+c4sin(2pi*x) to fit
def func(x, c1, c2, c3, c4):
return c1 + c2*x + c3*np.sin(np.pi*x) + c4*np.sin(2*np.pi*x)
popt, pcov = curve_fit(func, xi, yi)
x_fit = np.arange(0, 1, 0.01)
y_fit = func(x_fit, popt[0], popt[1], popt[2], popt[3])
# draw
plt.scatter(xi, yi, label='raw data')
plt.plot(x_fit, y_fit, label='fit curve')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
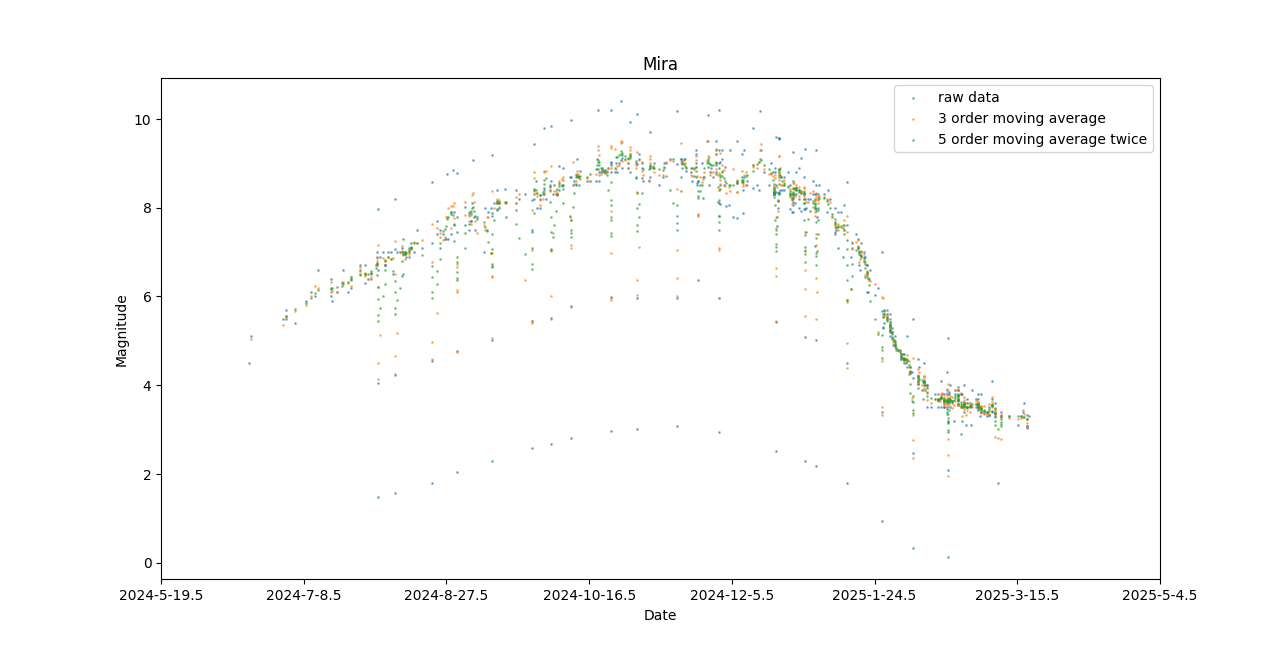
绘图结果如下:
T2: 滑动平均
题目
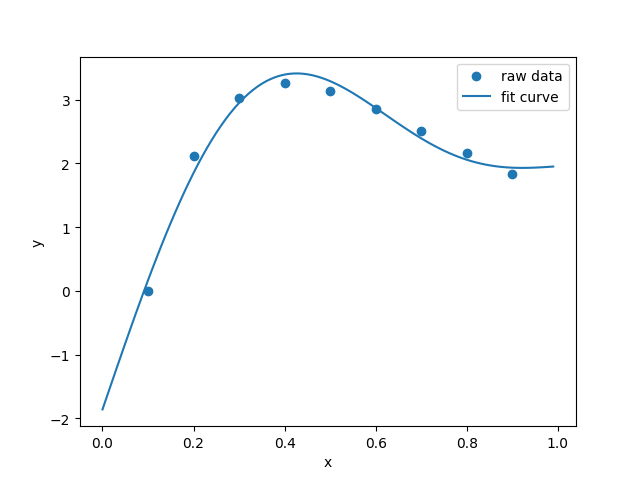
对 hw1 数据分别进行3阶滑动平均和5阶2次滑动平均,并讨论那种方式能更好地抑制主波动。
这里使用 hw1中的短期数据 进行分析
先对数组 mags 进行3阶滑动平均,即
再对数据 mags 进行5阶2次滑动平均,即
编写代码如下:
py
import numpy as np
import matplotlib.pyplot as plt
from jd import jd2ymd
# read data from data_short.txt
data = open('data_short.txt', 'r')
jds, mags = [], []
for line in data:
datas = line.split(',')
jd, mag = float(datas[0]), float(datas[1])
jds.append(jd)
mags.append(mag)
# 3 order moving average
n = len(mags)
mags_3 = []
for i in range(1, n-1):
now_mags_3 = (mags[i-1] + mags[i] + mags[i+1]) / 3
mags_3.append(now_mags_3)
# 5 order moving average twice
mags_5_1 = []
for i in range(2, n-2):
now_mags_5 = (mags[i-2] + mags[i-1] + mags[i]
+ mags[i+1] + mags[i+2]) / 5
mags_5_1.append(now_mags_5)
mags_5_2 = []
m = len(mags_5_1)
for i in range(2, m-2):
now_mags_5 = (mags_5_1[i-2] + mags_5_1[i-1] + mags_5_1[i]
+ mags_5_1[i+1] + mags_5_1[i+2]) / 5
mags_5_2.append(now_mags_5)
# draw scatter of data
plt.scatter(jds[:], mags[:], s=1, alpha=0.5, label='raw data')
plt.scatter(jds[1:-1], mags_3[:], s=1, alpha=0.5, label='3 order moving average')
plt.scatter(jds[4:-4], mags_5_2[:], s=1, alpha=0.5, label='5 order moving average twice')
# change the xticks from jd to date
xticks = plt.gca().get_xticks()
def change_ticks(val):
y, m, d = jd2ymd(val)
return f'{y}-{m}-{d}'
plt.xticks(xticks, [change_ticks(i) for i in xticks])
plt.title('Mira')
plt.xlabel('Date')
plt.ylabel('Magnitude')
plt.legend()
plt.show()1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
绘图结果如下: