原子物理
玻尔模型
里德伯公式
氢原子的谱线有经验公式
其中里德伯常数
各线系如下表:
| 线系名字 | |
|---|---|
| 赖曼系 | |
| 巴尔末系 | |
| 帕邢系 | |
| 布喇开系 | |
| 普丰德系 |
玻尔模型基本假设
- 定态假设
- 频率条件(辐射条件或玻尔准则): 电子跃迁释放光子
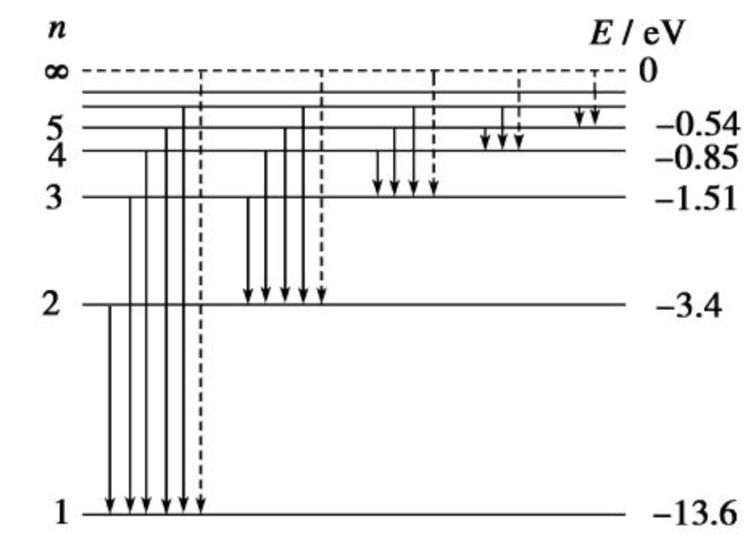
- 角动量量子化
玻尔模型
- 氢原子能量:
- 经典
- 量子
- 电子轨道半径
从光子(电磁辐射)频率导出电子轨道的另一表达式
- 经典
- 量子
得到
进而有
误差
理论值
实测值
- more:
- 玻尔半径
- 精细结构常数
- 电子轨道速度量子化
玻尔理论的修正
- 对原子核运动的修正
原子核不是静止的,考虑氢核和电子相对质心的运动, 所有出现电子质量
故里德伯常量
这与实验测量值
记
玻尔模型的结论
对于电子与微观粒子核两体绕转问题,记核为
该系统的里德伯常数
- 电子轨道半径
- 原子能量
常用的组合常数
玻尔理论的实验验证
- 类氢体系的光谱
- 氢的同位素
- 类氢离子
- 里德伯原子 (一个外层电子+一个带
- 类氢奇特原子
应用玻尔理论时做如下修正:
- 弗兰克-赫兹实验
证实原子具有分立的能量。
- 汞原子第一激发电势
实验装置如下图:
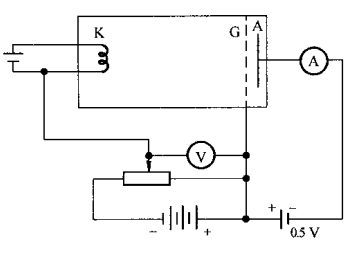
控制
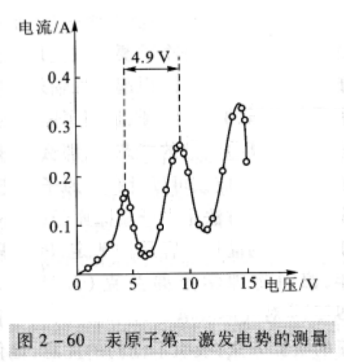
解释
- 在
- 在
- 电压
实验说明汞原子从基态到第一激发态的第一激发电势为
注
由于电子在
- 检验汞原子的其他能态
改进实验装置如下:
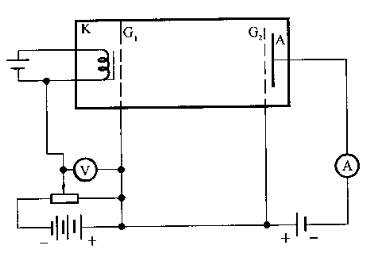
量子力学初步
波粒二象性
光的波粒二象性
康普顿散射实验
- 康普顿效应:被散射后的X射线,除了与入射X射线相同波长的成分,还多出了波长增大的成分,而且波长增加的大小随散射角的变化而不同。
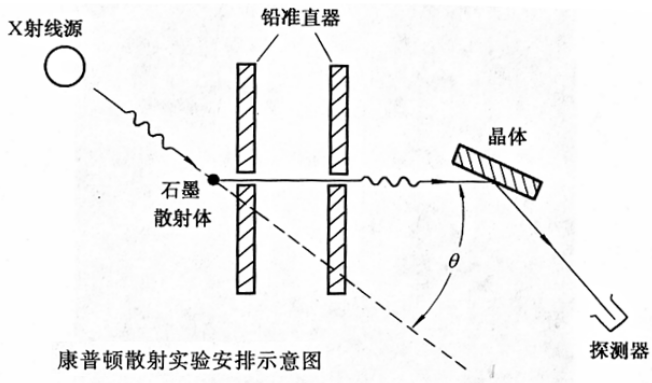
- 实验现象
- 新谱线相对原谱线的波长改变量
- 在同一散射角
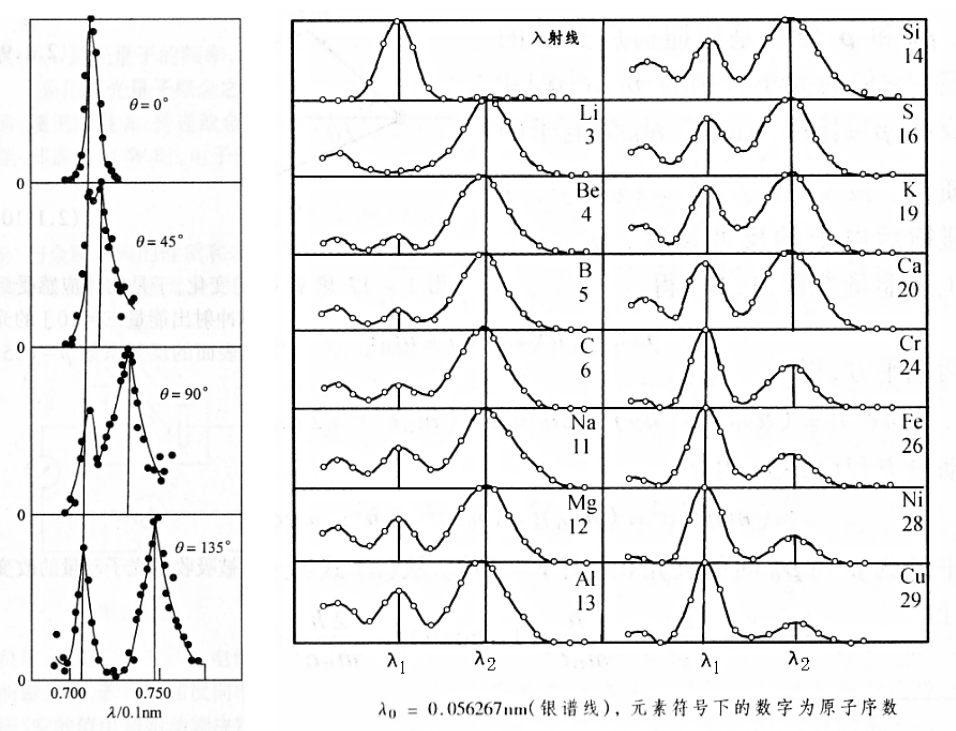
- 定性解释
- 当入射的高能光子与
- 当入射的高能光子与
- 定量解释
入射光子与自由电子发生弹性碰撞

可以得到
其中
相对论中粒子的能量和动量
粒子的总能量
质能动关系
动能动量关系
实物粒子波动性
- 德布罗意假设
- 我们可以观察到的宇宙是由光和实物组成的;
- 既然光具有波粒二象性,实物也可能具有这种波粒二象性;
- 德布罗意关系式:每一个具有静质量
写成与动能的关系
- 德布罗意波(物质波,实物波):一个具有确定能量
- 电子的晶体衍射实验
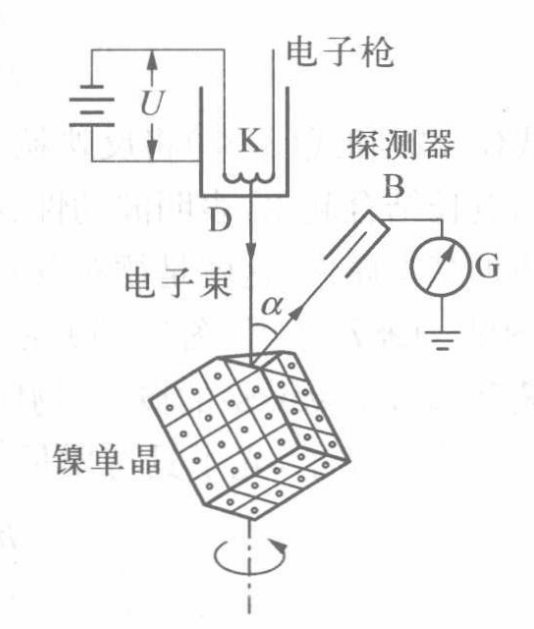
- 戴维孙-革末实验
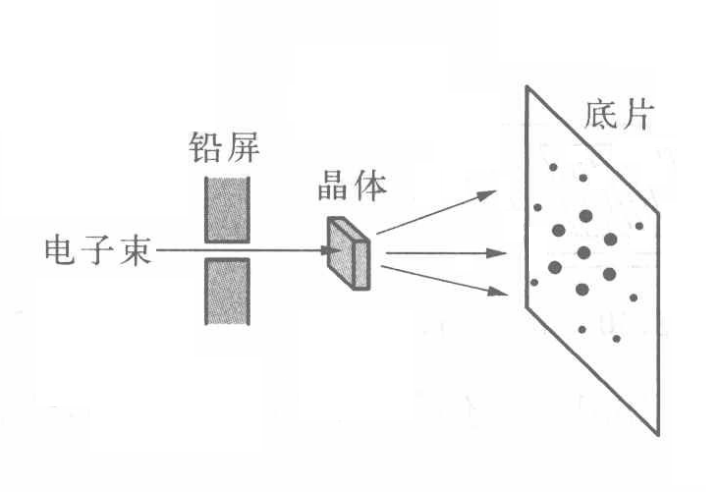
- 汤姆逊实验
量子力学第一假设
波函数及物理意义
微观粒子的波动性反映了其运动的统计规律:
波函数性质
- 标准条件:
- 归一化条件:
- 常数因子不定:
- 相干叠加性:若
也是这个系统的一个可能的量子态。
(波函数的态叠加原理,量子力学第一原理)
量子力学第二假设
薛定谔方程
对于一个静质量为
称为薛定谔方程。
定态薛定谔方程
当势场与时间无关,即
- 定态波函数
- 定态的薛定谔方程
量子力学第三假设
可观测量的平均值
可观测量算符表示
对任何一个可观测量
其中
量子力学第三假设:量子力学系统每个可观测量都对应着一个算符,可观测量可由相应的算符表示。
常见算符:
- 本征方程:
定态薛定谔方程
是哈密顿算符
量子力学第四假设
算符的对易关系
- 量子力学第四假设:表示微观体系力学量的算符之间有确定的对易关系。(量子条件)
- 广义不确定关系: 若两个力学量
位置动量不确定关系
- 微观粒子的同一方向的位置和动量的不确定度的乘积有下限,称为位置和动量的不确定关系(海森伯不确定关系)。
直角坐标系
极坐标系
能量时间不确定关系
这里
典型一维定态问题
一维无限深势阱
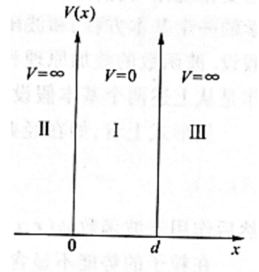
通过定态薛定谔方程求出波函数
其中
势垒和势垒贯穿
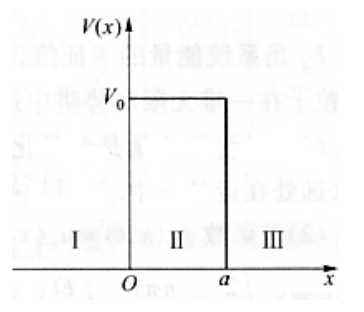
当
其中
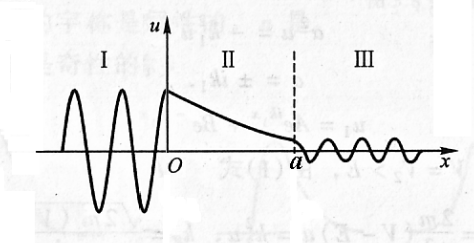
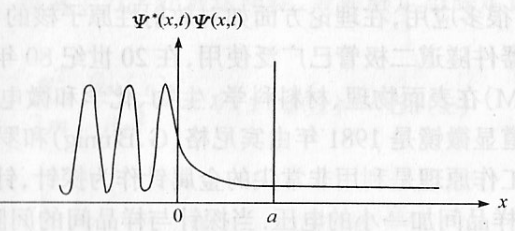
- 势垒贯穿:
- 透射系数:
当
氢原子与碱金属原子
氢原子
波函数
- 求解波函数
核:电荷
电子:电荷
势函数:
质心系下氢原子的定态薛定谔方程为
分离变量进行求解得:
其中主量子数
故
概率密度
- 角向分布:
- 径向分布
- 玻尔理论中的轨道半径
- 电子云图
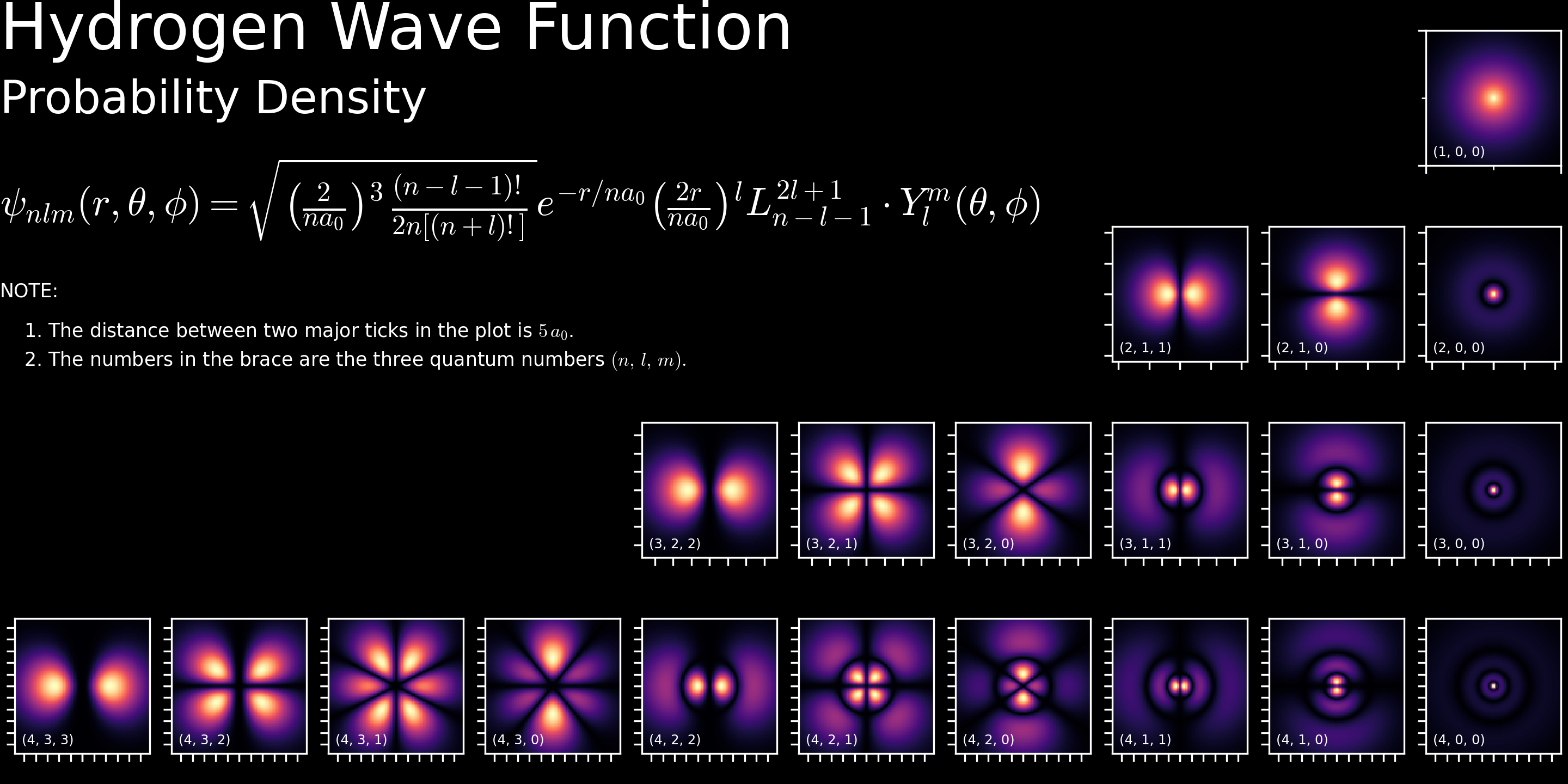
角动量
- 轨道角动量大小
角动量平方算符
本征值
则角动量大小
(
- 轨道角动量方向
- 角动量
- 轨道磁量子数:
- 角动量定义:
若一个算符包含三个分量
且它的三个分量满足如下基本对易关系
无论其物理意义如何,均可称为角动量算符。
- 角动量守恒:
在量子力学中,设力学量
则该力学量守恒。
量子数
- 轨道角量子数
- 其值习惯上用光谱学标记表示,
- 轨道磁量子数
- 主量子数
- 简并(degeneracy):不同的本征函数对应相同的本征值
能级
简并的本质是系统的对称性
- “球对称” 能量大小与
- “势函数
原子的辐射跃迁与选择定则
辐射跃迁
辐射跃迁:光子形式传递能量
碰撞跃迁:动能形式传递能量
谱线强弱因素:
- 相应能量的光子数
- 相应能级的跃迁原子数目
- 能级
跃迁的选择定则
- 选择定则:电偶极跃迁概率
- 允许跃迁(容许跃迁,allowed transition)
- 稳态(stable state)
- 允许线
- 禁戒跃迁(forbidden transition)
- 亚稳态(metastable state)
- 禁线(forbidden line),半禁线(semi-forbidden line)
- 宇称(parity):对波函数作空间反演
- 偶宇称:本征值
- 奇宇称:本征值
碱金属原子
光谱特点
锂原子的光谱:
- 主线系:波长范围最宽,第一条在可见光的红光区,其余均位于紫外;
- 第一辅线系:位于可见光区域,也叫漫线系,边缘模糊;
- 第二辅线系:位于可见光和红外区域,第一辅线系和第二辅线系的线系限相同,也叫锐线系,边缘清晰;
- 柏格曼系:位于红外区域,也叫基线系,频率最低。
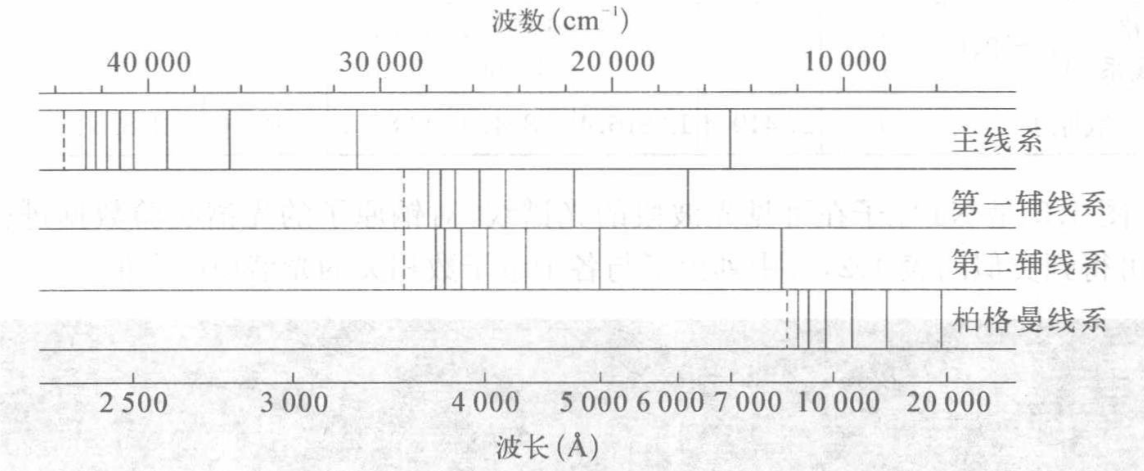
能级结构和允许跃迁
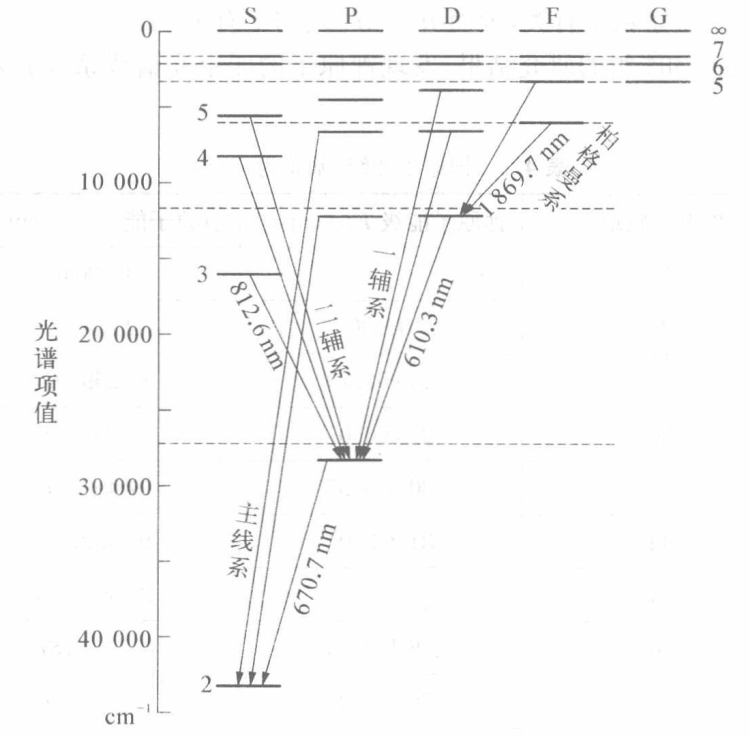
- 主线系:np->2s (principal 主)
- 一辅系:nd->2p (diffuse 漫)
- 二辅系:ns->2p (sharp 锐)
- 柏格曼系:nf->3d (fundamental 基)
光谱的理论解释
- 能级公式:
其中
- 原子实极化 & 贯穿效应
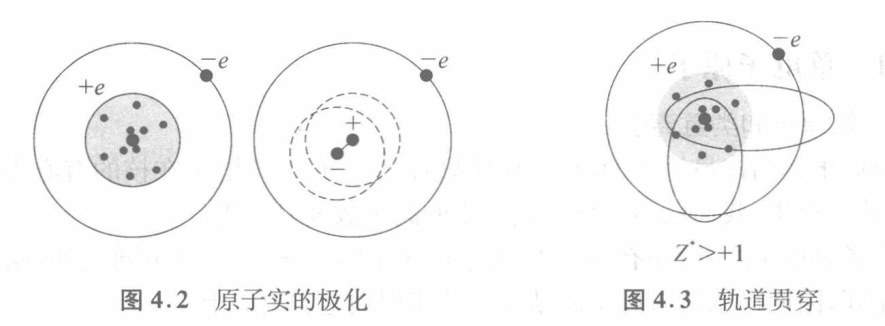
- 有效主量子数
- 量子数亏损(量子数修正)
- 屏蔽常数
- 波数公式
- 固定光谱项
- 跑动光谱项
- 碱金属光谱项
- 线系限:
- 共振线: np->ns 的光谱线
则锂原子的波数公式如下:
- 主线系
- 第一辅线系
- 第二辅线系
- 柏格曼系
电子的磁矩
电子的轨道磁矩
- 电子轨道磁矩
- 旋磁比(gyromagnetic ratio,或磁旋比 magnetogyric ratio)
- 电子的玻尔磁子
磁场中的电子轨道磁矩
- 磁矩与磁场的相互作用使系统具有磁势能
原子能量对磁量子数
- 在匀强磁场中,电子轨道磁矩
- 非匀强磁场中,一束原子垂直磁场方向入射,当
施特恩-格拉赫实验
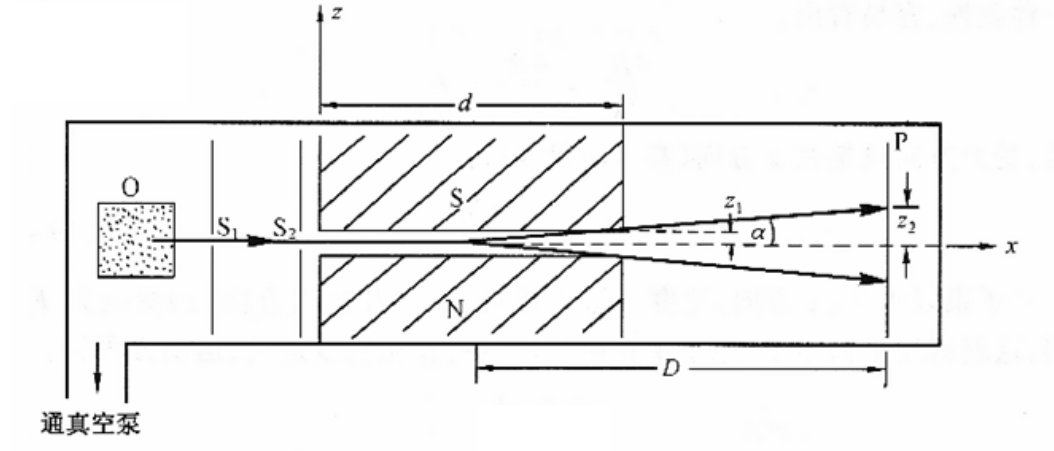
电子的自旋
- 自旋角动量量子数
- 自旋角动量
- 自旋角动量
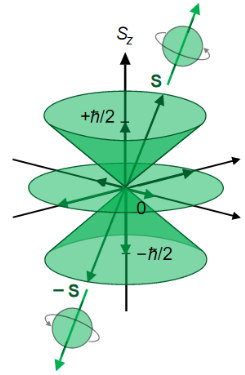
- 自旋磁矩
- 自旋磁矩
为了使同一粒子的各种角动量对应的磁矩在形式上一致,引入 g 因子( g-factor )
其中,
完全确定电子的状态需要 4 个量子数
自旋-轨道相互作用
角动量合成
对于两个角动量
合成的角动量
其中
单电子原子的总角动量
- 单电子原子的总角动量就是其价电子的总角动量
- 好量子数:在量子力学中,量子数是标记力学量本征值的指标。若该力学量是守恒量,那么对应的量子数就称为好量子数。
考虑自旋-轨道相互作用后的单电子原子,有 7 个量子数
单电子原子的总磁矩和有效磁矩
- 单电子原子的总磁矩是电子轨道磁矩和自旋磁矩的矢量和
其中
- 单电子原子有效磁矩是
其中
自旋-轨道耦合能
光谱的精细结构
- 粗结构 (gross structure) :只考虑电相互作用,忽略磁作用和相对论效应
- 精细结构 (fine structure) :考虑自旋-轨道相互作用
- 超精细结构 (hyperfine structure) :核自旋-电子耦合
碱金属原子光谱精细结构
粗结构
精细结构
精细结构的裂距
内 电子组态 (electron configuration) :基态钠原子
电子态符号 (electronic term symbol)
原子态符号 (term symbol)
- 结构特点及实验验证
- 精细结构的多重线特征:
双重线: 主线系
三重线: 一辅系
- 选择定则:
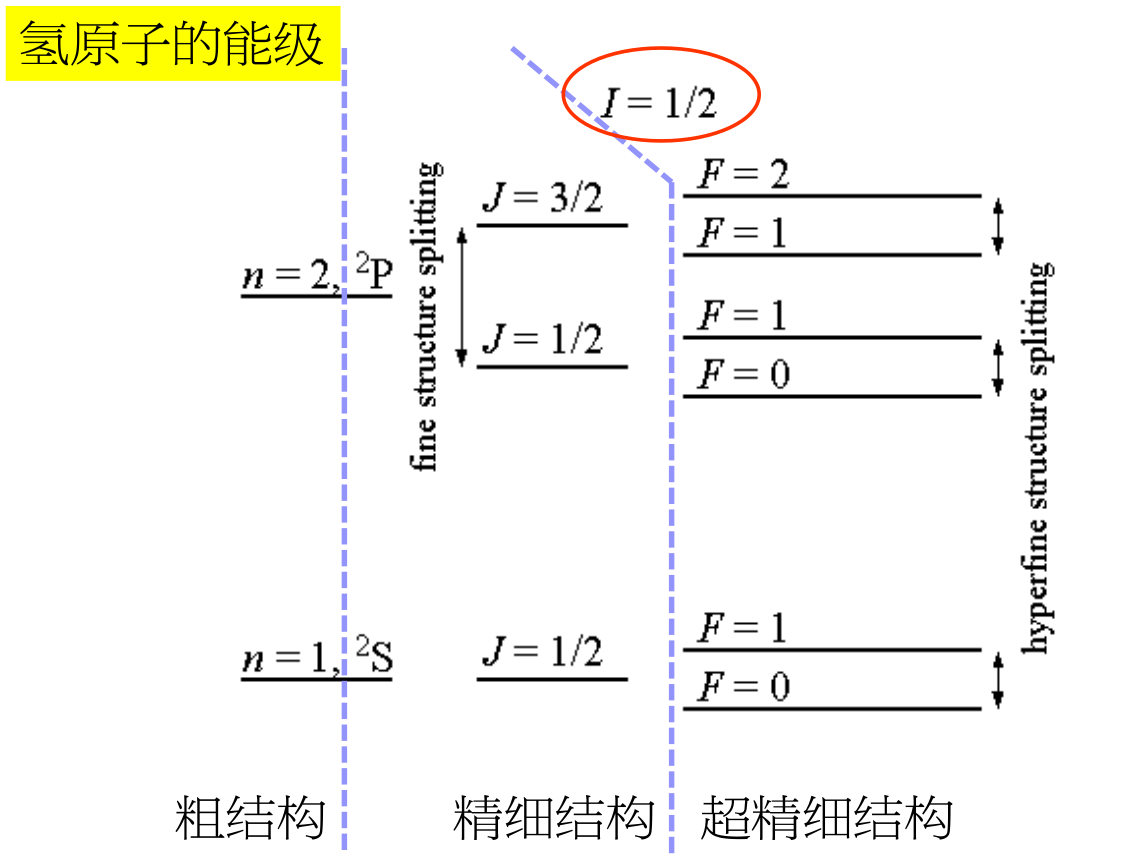
氢原子光谱精细结构
- 粗结构
- 精细结构
- 电子自旋-轨道相互作用能
- 电子绕核运动动能的相对论修正
- 库仑势的相对论修正(达尔文项)
- 氢原子的精细结构项 (fine structure)
- 一级近似下,氢原子的能量公式
- 实验观测
对
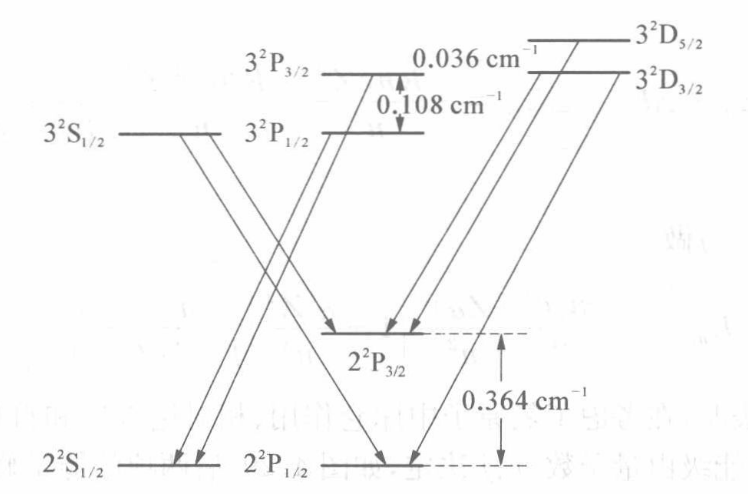
- 兰姆位移 (Lamb shift)
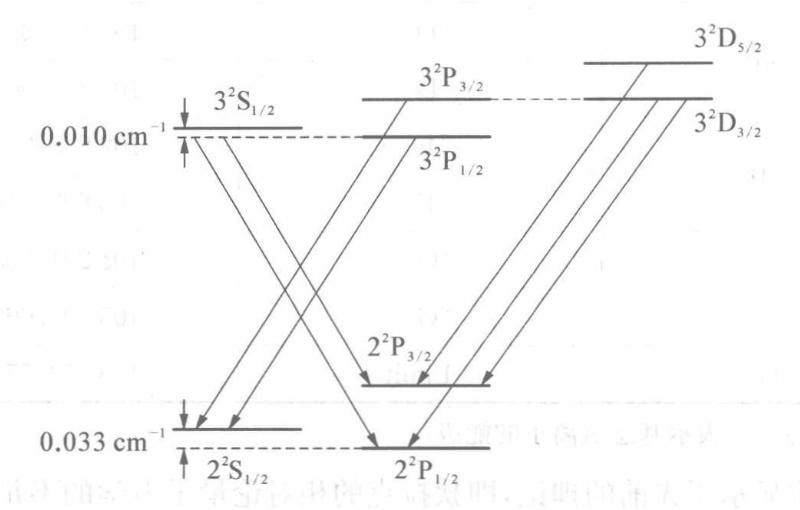
- 氢原子的超精细结构 (hyperfine structure)
考虑核磁矩
多电子原子
中心力场近似
- 中心力场近似 (central field approximation) :
假设原子中某电子
包含了两个假设:1. 独立电子模型;2. 中心力场近似。
- 剩余库仑相互作用
哈密顿算符
零级近似的哈密顿量
原子总能量为
泡利不相容原理
- 泡利不相容原理 (Pauli Exclusion Principle) :
在原子中,要完全确定一个电子的状态,需要四个量子数。原子中任意两个电子的这四个量子数不能完全相同。或者说,每个量子态只能容纳一个电子。
全同粒子 (identical particles) :内禀性质完全相同的粒子。
量子力学第五基本假设:在全同粒子组成的多粒子体系中,全同粒子具有不可分辨性;交换任意两个粒子不会引起体系物理状态的变换;体系的波函数具有交换对称或反对称性。(微观粒子的全同性原理)
考虑一个双粒子全同粒子体系(如氦原子),记两个粒子分别为
- 满足 (1) 式的波函数称为交换对称波函数。如光子、胶子、声子、引力子、氦原子等自旋量子数为整数的全同粒子体系波函数。在统计物理中,这些粒子遵从玻色-爱因斯坦统计,称为玻色子 (bosons)
- 满足 (2) 式的波函数称为交换反对称波函数。如电子、质子、中子、中微子、夸克等自旋量子数为半奇数的全同粒子体系波函数。在统计物理中,这些粒子遵从费米-狄拉克统计,称为费米子 (fermions)
- 不相容原理更普遍的表述:费米子组成的全同粒子体系的波函数一定是交换反对称的。这种全同费米子体系的每个量子态只能容纳一个费米子。
原子的粗结构能级和壳层结构
原子的壳层结构
- 主壳层 (shell) 主量子数
- 支壳层 (subshell) 相同
- 同一支壳层最多容纳电子数
- 同一壳层最多容纳电子数
- 闭合壳层 (closed shell) (满壳层):被电子填满的壳层。
- 闭合壳层特点:1. 电子电荷分布球对称;2. 总角动量和总磁矩均为零。
原子的电子组态
- 电子组态 (electron configuration) (电子构型、电子排布) e.g. 氧原子
- 基组态:原子能量最低电子组态
- 激发组态:非基组态
元素周期表与电子基组态
决定原子的电子基组态原则:
- 泡利不相容原理
- 能量最小原理
- 第一周期:对应主壳层
- 第二周期:主壳层
- 第三周期:主壳层
- 第四周期:主壳层
- 第五周期:
- 第六周期:
- 第七周期:
洪德定则(经验规律):电子在填充支壳层时,首先会选择自旋方向向上(即
多电子原子能级精细结构
多电子原子的粗结构
多电子原子的精细结构
- 电作用:剩余库仑作用
- 磁作用:电子自旋-轨道相互作用
LS耦合
以双价电子体系为例
在中心力场近似(能级粗结构)的基础上,LS耦合分两步:
多重态 (multiple state) 修正:
主要的相互作用发生在不同原子之间。
设两个电子的轨道角动量分别为
则原子的总轨道角动量
其中,总轨道角动量量子数
相应的磁量子数
类似的,原子的总自旋角动量
其中,总自旋角动量量子数
相应的磁量子数
更一般的,当有
多重态能级用谱项(符号)
精细结构修正:
考虑
则原子的量子态由量子数
LS耦合的精细结构能量公式为
用光谱支项符号
- LS耦合的两个定则:
朗德间隔定则:
同一多重态的精细结构中,两个相邻能级的间隔与他们中较大的
洪德定则 (Hund's rules):
在同一电子组态形成的原子态中,首先看
当
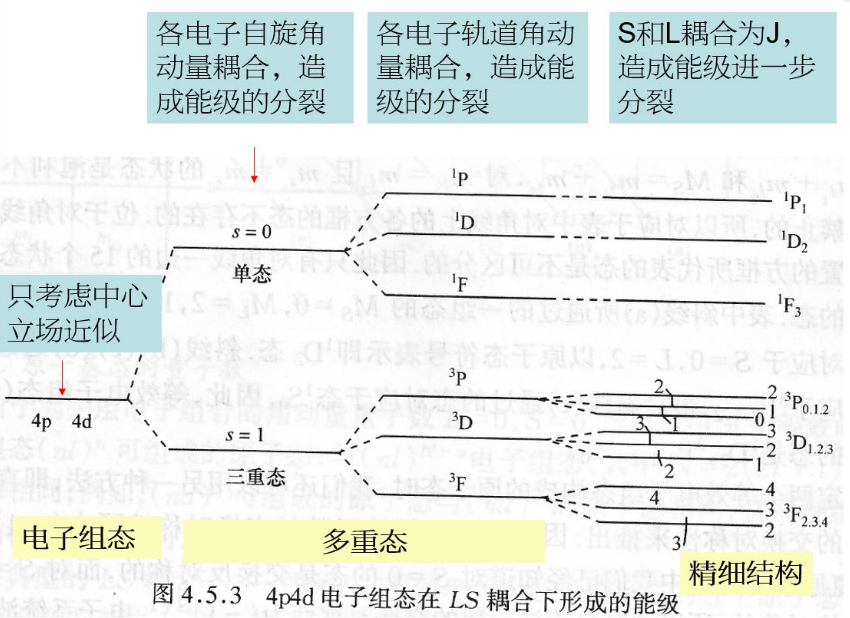
- 等效电子 (equivalent electrons):
- 非等效电子/非同科电子
jj耦合
第一步修正: 每个电子的轨道角动量
第二步修正: 各个电子的总角动量耦合成原子的总角动量
原子态表示为
多电子原子的实验光谱
选择定则
电子组态的选择定则
- 奇宇称
- 偶宇称
电子组态的选择定则为
- 奇宇称
原子态的选择定则
- LS耦合(原子态
除 外 外 磁 场 环 境 中 - jj耦合(原子态
或 除 外 外 磁 场 环 境 中 - LS耦合(原子态
氦原子的光谱
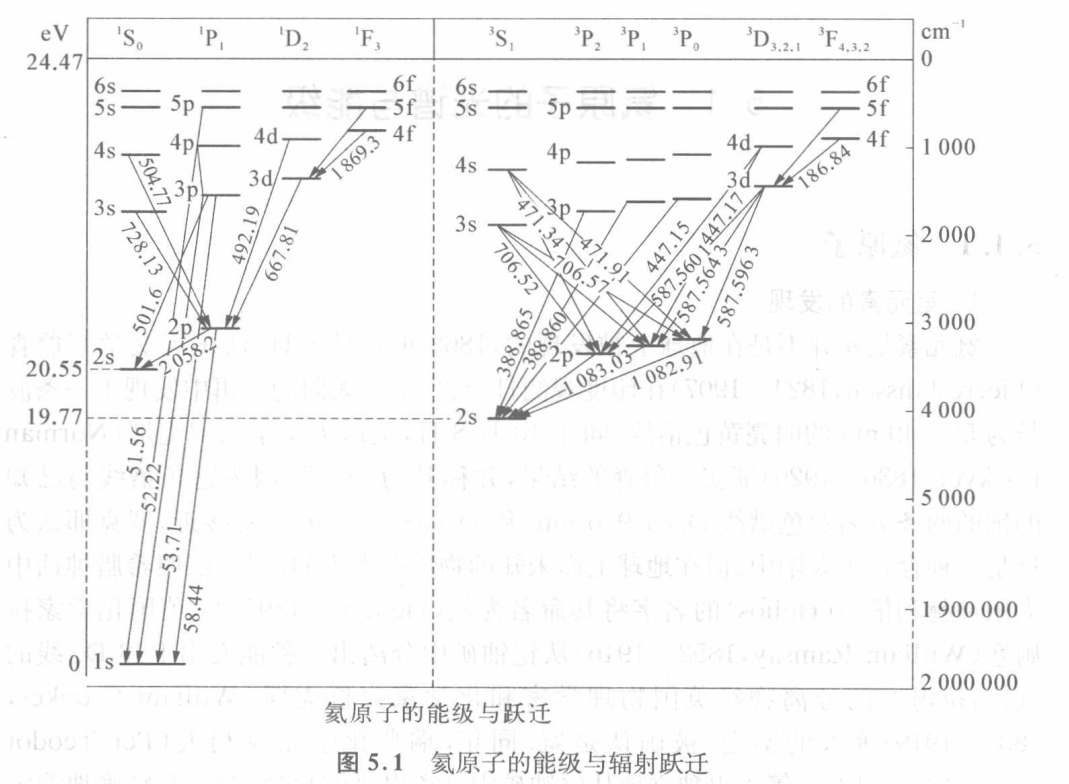
- 仲氦 (Parahelium) :发射单线结构光谱
- 正氦 (Orthohelium) :发射三重线光谱
X射线谱与原子内壳层结构
X射线谱线源自于原子内层电子能级的跃迁
X射线管
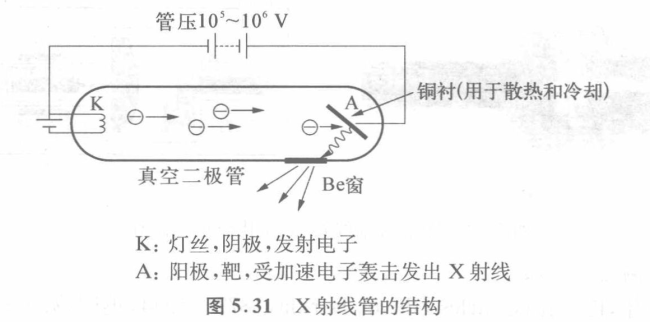
X射线光谱
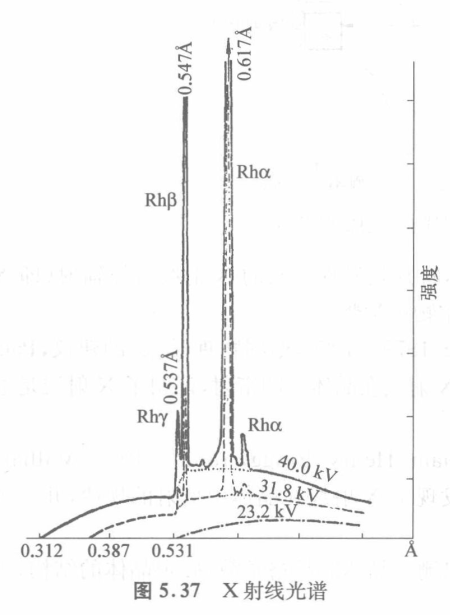
- 连续谱:由轫致辐射(刹车辐射)(自由-自由跃迁)
- 短波限:
- 特征谱/标识谱:激发电压,线系分为
- 莫塞莱定律:特征谱波数公式